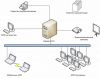
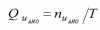Оптимизация процесса планирования полетов при летных испытаниях
Содержание:
- Выбор математических методов для решения частных оптимизационных задач планирования полетов
- Критерий минимума продолжительности летной смены
- Критерий максимума ранжирования приоритета тем
- Вывод
- Литература
Статья написана по материалам конкретных исследований, направленных на совершенствование системы планирования летных экспериментов. В ней впервые приведены пути оптимизации данной системы по задаваемым критериям. Результаты работы внедрены в автоматизированной системе планирования полетов при летных испытаниях авиационной техники.
На этапе предполетной подготовки наиболее сложным и трудоемким процессом является оптимальная расстановка испытательных полетов (летных экспериментов) в плановой таблице (ПТ) в соответствии с критериями, ограничениями и функциональными взаимосвязями.
Для решения оптимизационной задачи планирования полетов следует воспользоваться методом декомпозиции и разбить ее на четыре этапа:
- разработка процедуры приведения частных оптимизационных задач к постановке, в которой могут использоваться классические математические методы оптимизации;
- модификация существующего алгоритма расстановки полетов;
- решение частной задачи расстановки полетов;
- разработка алгоритма и итогового метода решения оптимизационной задачи планирования полетов.
На первом этапе производится анализ существующей системы расстановки испытательных полетов (летных экспериментов) в ПТ, сопоставление потребностей с имеющимися в настоящий момент возможностями, деление на частные задачи оптимизации. Некоторые из параметров, характеризующих потребности и возможности, имеют заранее известные значения (программы испытаний, уровень подготовки летного состава и т.д.), некоторые - носят случайный характер (метеоусловия, исправность самолетов к определенному часу и т.д.). В результате анализа представляются методы решения частных задач оптимизации по соответствующим критериям.
На втором этапе рассматривается модификация существующего неавтоматизированного алгоритма планирования испытательных полетов применительно к автоматизированным распределенным системам.
На третьем этапе, абстрагировавшись от частных задач оптимизации, производится решение частной задачи оптимальной расстановки испытательных полетов в плановой таблице.
На четвертом этапе производится объединение решений, полученных на первых трех этапах. В результате модификации алгоритма, комплексирования методов решения частных задач и метода решения задачи оптимальной расстановки всех полетов получается итоговый метод решения оптимизационной задачи планирования полетов (летных экспериментов).
Выбор математических методов для решения частных оптимизационных задач планирования полетов
Базовыми параметрами, используемыми при планировании летных экспериментов, являются: темы, воздушное пространство, полигоны, парк самолетов (вертолетов) и летный состав. Оптимальное распределение вышеуказанных параметров в соответствии с существующими критериями и наложенными ограничениями может быть произведено при помощи различных математических моделей и соответствующих им методов. Применимость модели к решению определенной задачи зависит от количества рассматриваемых показателей, характеризующих модель, т.е. от размерности модели. Разработка имитационных моделей большой размерности позволяет получить увеличение степени оптимальности рассматриваемой части системы, но при этом ведет к значительному усложнению имитационной модели.
Критерий минимума продолжительности летной смены
Главным критерием при планировании полетов (летных экспериментов) является минимизация продолжительности летного дня:
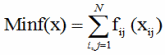
, (0)
при условии, что ![]()
,
где N – количество полетов,
Gij - ограничения, накладываемые на полеты.
Двойная индексация переменных обусловлена спецификой формирования плана полетов, а именно: fij(xij) равно разности между временем взлета (посадки) i-го самолета и временем взлета (посадки) другого, j-го самолета. В один и тот же момент времени с взлетно-посадочной полосы (ВПП) не могут взлетать или садиться 2 самолета – минимальный интервал времени равен 2,5 мин. Это время соответствует продолжительности посадки и сруливания летательного аппарата с ВПП или времени выруливания на ВПП, взлета и ухода на безопасное расстояние. Таким образом, минимальное время летной смены (в минутах) без учета продолжительности полетов, составляет:
fmin(x) = 2х2,5хN = 5хN.
При максимальной продолжительности летной смены в 10 часов (т.е. 600 мин) количество полетов, которое может быть выполнено за одну смену (без учета времени продолжительности полетов), не может превышать 120. При наложении ограничения, определяемого продолжительностью полетов, максимальное количество полетов, которое можно запланировать, будет значительно меньше. Продолжительность каждого полета является заранее известной величиной и определяется выполняемыми упражнениями и выделенным на полет топливом. Кроме этого, для различных видов полетов средняя продолжительность одного полета следующая:
- для испытательных полетов – 60-120 мин;
- для вспомогательных полетов – 60-120 мин;
- для прочих полетов – 20-60 мин.
Кроме того, испытательные полеты составляют примерно 40% от общего количества полетов, вспомогательные – 20%, а прочие – 40% от общего количества полетов.
Все вышеуказанные ограничения в значительной мере влияют на продолжительность летной смены, при этом задача поиска экстремума критериальной функции (1) не может быть отнесена как к задачам линейного программирования, так и к задачам нелинейного программирования. В то же время эта задача может быть решена одним из методов последовательного анализа вариантов, например методом прямого перебора.
Классические методы решения задач последовательного анализа вариантов с ограничениями характеризуются тем, что чем больше ограничений наложено на область изменения аргумента критериальной функции, тем сложнее становится задача оптимизации – тем труднее найти ее решение с помощью обычных методов. С другой стороны, задача отыскания значения аргумента, доставляющего максимум критериальной функции, должена быть тем проще, чем уже допустимая область изменения аргумента. Если ограничения настолько жесткие, что это множество сводится к нескольким точкам, то методом последовательного анализа эти точки легко отыскать, а их перебор дает быстрое нахождение оптимального значения. В общем случае, формулировка задачи поиска оптимального значения функции методами последовательного анализа вариантов может быть записана в следующем виде [1]:
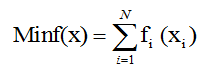
,
где xi - скалярные компоненты вектора x, причем этот выбор стеснен ограничениями:
![]()
Если обозначить через Ω множество всех допустимых векторов, то можно обозначить как ω1 множество всех векторов х из Ω, у которых первая компонента не доставляет максимум функции f1(x1) на множестве G1. Очевидно, что искомый вариант не может содержаться в ω1. В самом деле, какой бы вариант:
![]()
Увеличить getmancev082008-5.gif (2кб)
не был бы взят, его сразу можно улучшить. Значение f(x0), где х0={x1,x2,…,xN*}T, будет меньше, чем f(x*). Таким образом, оптимальный вариант содержится среди векторов, принадлежащих множеству:
Ω1=Ω|ω1.
Было произведено сужение множества вариантов – от множества Ω перешли к множеству Ω1. Повторяя рассуждения, в конце концов, получается множество:
ΩN=Ω|ω1|ω2| … |ωN,
содержащее векторы:
x={x1,x2,…,xN},
каждый из которых является решением задачи.
Характер рассуждений при решении этой задачи определяется не только функцией f(x), но также и ограничениями G. Описанный процесс можно интерпретировать как построение некоторого дерева решений, ветви которого последовательно анализируются и отсекаются. Существует несколько методов решения задач последовательным анализом вариантов. Применимость каждого из них определяется заданной точностью и вычислительной сложностью достижения результата.
Критерий максимума ранжирования приоритета тем
Вторым по значимости критерием после минимизации продолжительности летной смены является критерий максимального ранжирования приоритета тем, т.е. испытательные полеты (летные эксперименты) с наивысшим приоритетом должны выполняться в первую очередь. Формализуя основные требования по выполнению ранжирования приоритетности тем, потребуем выполнения двух условий: все полеты должны быть расставлены строго по приоритету и наиболее важные темы однозначно должны войти в плановую таблицу полетов.
Наиболее приоритетные темы (Pi=1) должны получить наибольший вес, менее приоритетные (Pi=N) – наименьший. Это соответствует условию выполнения полетов по наиболее важным темам в ходе летного дня. Для темы i ее весовой коэффициент Ci определяется по формуле:
Ci= /Pi, (0)
По этому критерию все важные полеты должны попасть в плановую таблицу:

, (0)
где i – номер темы в перечне, i=1, 2, …, N;
N - количество тем;
Pi – номер темы в перечне приоритетов специальных работ.
Кроме вышеуказанного условия (3), важным является условие совпадения очередности выполнения тем с их приоритетом:
Si = ABS (i - Pi), (0)
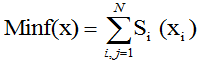
, (0)
где ABS – функция модуля числа.
Обобщая два вышеуказанных условия (2, 4) и считая, что ΣCi→Max, ΣSi→Min (3, 5), получим итоговую критериальную функцию по определению оптимальности расстановки тем испытательных полетов в плановой таблице:
fi(xi) = Si/Ci,
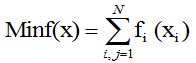
, (0)
В идеальном случае критериальная функция f(x) равна нулю, т.е. все полеты расставлены строго по приоритету и наиболее важные темы вошли в плановую таблицу полетов. На рис. 1 представлена диаграмма с показателем, характеризующим степень отклонения порядка расстановки полетов от перечня приоритетов тем (ΣSi), и показателем, отражающим степень вхождения наиболее важных тем в плановую таблицу полетов Σ (Si/Ci). Наиболее рациональным является 1 вариант расстановки полетов, в котором все полеты ранжированы строго по перечню приоритетности тем.
Для быстрого выявления тем, которые резко не соответствуют перечню приоритетов, может быть использовано отношение двух данных показателей:
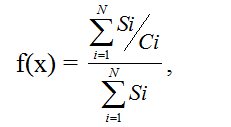
, (0)
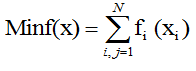
, (0)
при условии, что знаменатель не равен нулю, т.е. ![]()
Si≠0. Оптимальный 1 вариант расстановки полетов при расчете данного показателя не используется, т.к. для него ![]()
Si=0. Назовем отношение (7) смешанным показателем.
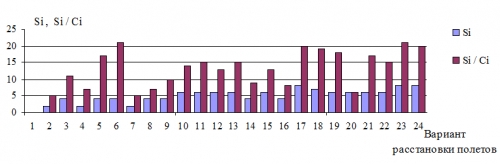
Увеличить getmancev082008-12.gif (8кб)
Рис. 1. Показатели правильность расстановки полетов в соответствии с перечнем приоритетных тем
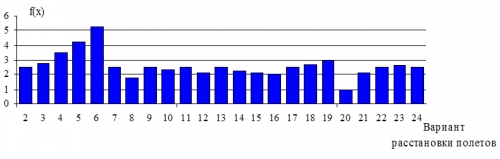
Увеличить getmancev082008-13.gif (7кб)
Рис. 2. Смешанный показатель правильности расстановки полетов в соответствии с перечнем приоритетных тем
Превышение среднего уровня в данном отношении соответствует вхождению в ПТ полета с номером темы, значительно отличающегося от номера, который должен быть при строгой расстановке полетов по приоритетности тем (рис. 2, вариант 6).
Таким образом, при поиске оптимального значения методом последовательного анализа вариантов в качестве критериальных функций могут выступать функции (3), (5), (6) или (8). При этом наиболее предпочтительным является использование функции (8). Расстановка полетов в соответствии с приоритетностью выполнения тем так же, как и расстановка полетов с целью минимизации продолжительности летной смены, должна быть описана моделью, использующей метод последовательного анализа вариантов. Стоит отметить, что вспомогательные полеты имеют тот же вес, что и соответствующие им полеты на испытания. Все резервные полеты, в том числе и все прочие полеты, имеют нулевой вес. Таким образом, производится поиск такого оптимального варианта в многогранном пространстве ограничений, при котором критериальная функция достигает экстремума – минимум соответствует наилучшему способу распределения полетов по темам.
Критерии оптимального распределения воздушного пространства, летного состава и самолетного парка
Наиболее адекватно процессы деления воздушного пространства, летного состава и самолетного парка могут быть описаны в терминах транспортной задачи, для решения которой существует большое количество стандартных методов [2]. Поэтому нет необходимости приводить здесь подробное решение частных оптимизационных задач.
Из рассмотренного материала видно, что разработка и оптимизация ПТ полетов носит последовательный, многоитерационный характер. Методами системного анализа определяются входные переменные и исходные значения параметров. Объединение параметров в итоговое решение производится в зависимости от степени их влияния на соответствующие критериальные функции. Весовые коэффициенты, оценочные значения параметров влияния и показатели эффективности определяются эвристическим способом методом экспертных оценок. В результате проведения многокритериальной оптимизации ПТ полетов происходит сокращение продолжительности летного дня на 10-15% при условии включения в ПТ всех запланированных полетов. Это делает возможным на 10-15% увеличить количество испытательных полетов, выполняемых за летную смену, что дает весомый экономический эффект за счет сокращения календарных сроков испытаний.
1. Аоки М. Введение в методы оптимизации. Основы и приложения нелинейного программирования. – М.: Наука, 1977. – 342 с.
2. Исследование операций. Под ред. Дж. Моудера, С. Элмаграби. В 2 т. - М.: Мир, 1981. – 2 т.