Многофакторная оптимизация методом случайного поиска
В статье рассмотрен метод случайного поиска при решении задачи многофакторной оптимизации и повышения надежности воздушных судов в экстремальных условиях.
Применение метода случайного поиска многофакторной оптимизации обусловлено тем, что нет необходимости вычислять первые и вторые производные функции цели (в отличие от градиентных методов), что особенно трудно, если выражение целевой функции сложное. Кроме того, алгоритм случайного поиска позволяет достаточно просто учитывать ограничения на область изменения переменных. Доработка алгоритма случайного поиска специальной процедурой позволяет выявить с большой достоверностью все локальные и условные экстремумы и выбрать из них глобальный. Применение в случайном поиске самообучения (адаптации) по направлению поиска и длины рабочего шага позволяет обеспечить приемлемую оперативность решения.
Алгоритм оптимизации функции цели методом случайного поиска составлен на основе рекомендаций. Он позволяет решать следующие задачи:
- выбор начальных точек поиска;
- организацию траектории поиска из начальных точек до пересечения с границей области;
- выявление локальных и условных минимумов;
- определение глобального минимума.
Выбор начальных точек осуществляется случайным образом при условии принадлежности их к границе области, задаваемой системой неравенств (функций ограничений) вида:
![]()
(1)
Обычно, даже при достаточно сложной многомерной гиперобласти параметров для надежного поиска глобального оптимума, достаточно 5...10 начальных точек.
Из каждой текущей точки траектории осуществляется "m " случайных проб:
![]()
Увеличить ruhlinskiy2008-2.gif (3кб)
(2)
где α - рабочий шаг,
![]()
- случайный вектор, спроектированный на единичную гиперсферу.
Для определения наиболее вероятного статистического градиента изменения функции цели рекомендуется выбрать m = 25...30.
Переход в новую (k+1) точку траектории осуществляется в соответствии с выражением:
![]()
(3)
где j – номер пробы, в которой значение целевой функции наименьшее из всех “m” случайных проб.
Тогда
![]()
Увеличить ruhlinskiy2008-5.gif (5кб)
(4)
где x – индикаторная функция, определяемая из следующих соотношений:
![]()
Увеличить ruhlinskiy2008-6.gif (12кб)
(5)
Индикаторная функция x определяет возможность движения по траектории при удачном шаге, тогда x=1, или запрещает переход в новую точку поиска при x=0.
Выход за допустимую область ![]()
рассматривается как неудачный шаг.
Для обеспечения продолжения поиска по траектории после нахождения локального экстремума в качестве минимизирующей функции принято:
- на спуске у*=у;
- на подъеме у*=у.
Если шаг был неудачным (x=0), то переход в новую точку не происходит, а поиск повторяется из одной и той же точки, но с меньшим шагом.
Алгоритмом предусмотрена адаптация рабочего шага в ходе поиска по следующему соотношению:

Увеличить ruhlinskiy2008-8.gif (9кб)
(6)
Таким образом, величина шага увеличивается, если в предыдущей точке произошло уменьшение значения функции цели, и уменьшается, если в предыдущей точке не произошло ее уменьшения.
γ1,γ2 – параметры алгоритма, которые должны удовлетворять условию:
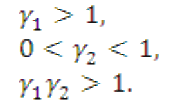
(7)
Величина αk оптимальная, если отношение количества удачных шагов по всем шагам равна Pn*. Величина Pn* характеризует вероятность удачного шага. Численное значение этого параметра лежит в диапазоне 0,14...0,27.
В этом случае для выбранного значения γ1(обычно 1,2 – 1,7) γ2 определяется выражением:

(8)
При прохождении по траектории фиксируются все точки локальных минимумов:
![]()
(9)
если , ![]()
Увеличить ruhlinskiy2008-12.gif (4кб)
и перевалов:
![]()
(10)
если ![]()
Увеличить ruhlinskiy2008-14.gif (4кб)
Условием оптимума является уменьшение величины неудачного шага меньше заданной величины:
![]()
(11)
После пересечения траектории с границей области

(12)
выбирается (случайным образом) начальная точка для следующей траектории. После прохождения 5...10 траекторий из всех выявленных локальных минимумов и границ траекторий определяется глобальный оптимум
![]()
(13)
Для повышения быстродействия поиска предусмотрена его адаптация, заключающаяся в увеличении плотности распределения случайных векторов в направлении наиболее вероятного уменьшения цели ![]()
Такое увеличение плотности распределения осуществляется за счет введения параметра β, который определяет степень детерминированности процесса поиска, а также за счет ортонормированного преобразования случайного вектора ![]()
, равномерно распределенного на единичной сфере таким образом, что новая реализация случайного вектора ![]()
определяет точку, которая лежит между определяемыми векторами:
![]()
(14)
и ![]()
(15)
Параметр определяется из следующих рекурентных соотношений:
![]()
Увеличить ruhlinskiy2008-22.gif (20кб)
(16)
Численные характеристики случайного вектора ![]()
, математическое ожидание и среднеквадратичное отклонение деформируются от равномерного распределенного на единичной гиперсфере по зависимостям:
![]()
(17)

- при неудачном шаге; (18)
по зависимостям:
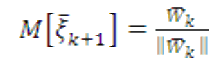
(19)

- при удачном шаге. (20)
Степень деформированности определяется выбором начального значения β. Чем ближе β к «I», тем процесс менее детерминирован.
В работе рекомендуется принимать начальное значение β=5...10. Таким образом, адаптация алгоритма оптимизации позволяет по мере движения по траектории к минимуму сужать раствор гиперконуса варьируемых параметров, в котором осуществляется поиск, и увеличивать длину рабочего шага (увеличением значений «β» и «α»). При приближении к минимуму (неудачные шаги) рабочий шаг уменьшается, а поиск осуществляется в гиперсфере. При нахождении минимума для быстрейшего выхода на точку перевала помимо изменения целевой функции на обратную направление поиска осуществляется в узком конусе с β=β0 и постоянным шагом «α0».
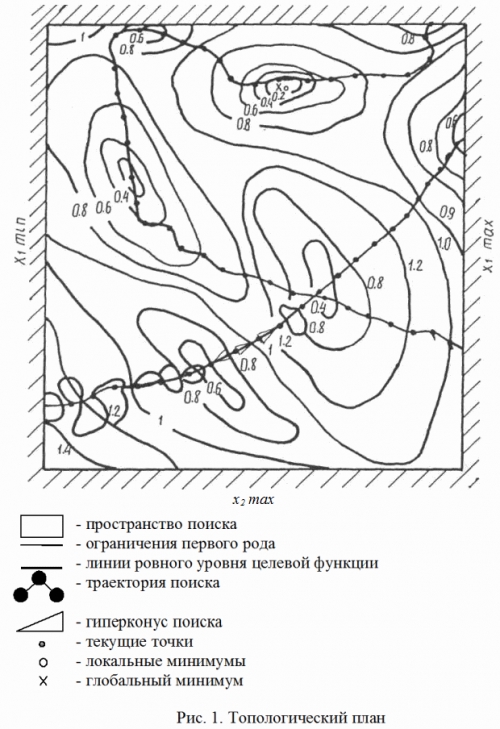
На рис. 1 показан топологический план поиска функции двух переменных. На рис. 2 приведены схемы адаптации шага и направление поиска.
Увеличить ruhlinskiy2008-28.gif (70кб)

Увеличить ruhlinskiy2008-29.gif (31кб)
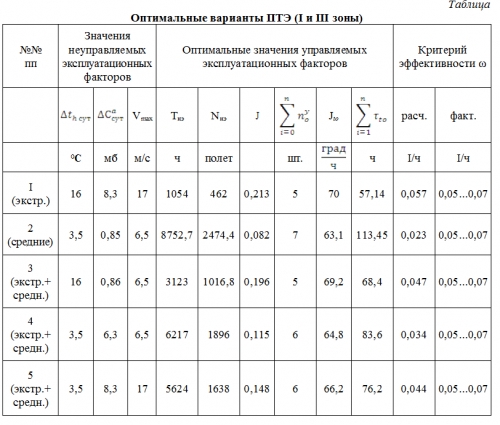
В результате оптимизации процесса эксплуатации по рассмотренному алгоритму получены оптимальные варианты сочетания неуправляемых и управляемых эксплуатационных факторов, обеспечивающие минимальный параметр потока отказов ВС (табл.).
Увеличить ruhlinskiy2008-30.gif (32кб)
Как видно из табл. в указанном диапазоне изменения параметров процесса можно достигать снижения параметра потока отказов более чем в 2 раза (см. строку 2). При этом варианты сочетаний эксплуатационных факторов характеризуются следующим образом:
- строка I - экстремальные значения (встречаются крайне редко);
- строка 2 - средние значения, типичные для влажной зоны Крайнего Севера и Арктики;
- строки 3, 4, 5 - сочетания средних и экстремальных значений.
Анализ представленных результатов оптимизации, полученных расчетным путем, позволяет сделать следующие выводы:
1) наибольшее влияние на параметры безотказности ВС оказывают факторы: наработка ВС с начала эксплуатации, интенсивность эксплуатации, интенсивность подогрева, «глубокие» переходные циклы охлаждения ВС, длительное время нахождения ВС в нерабочем состоянии на стоянках;
2) влияние экстремальных и средних значений факторов Крайнего Севера и Арктики, и соответствующие им оптимальные расчетные значения управляемых эксплуатационных факторов, требуют дифференцированного установления назначенного ресурса авиационной техники в зависимости от региона базирования ВС. Для экстремальных условии эксплуатации оптимальные расчетные значения назначенного ресурса 1-ой группы самолетов Ту-134А составляют 1054 л.ч., 462 полета, для средних условий - 8752 л.ч, 2474 полета;
3) экстремальные условия эксплуатации требуют сокращения времени нахождения ВС в нерабочем состоянии, в котором его «эффективная температура» находится в области низких температур;
4) на ВС существенное влияние оказывают «глубокие» переходные циклы охлаждения конструкции, их интенсивность и повторяемость (количество). Чем больше «глубоких» переходных циклов, тем ниже уровень надежности авиационной техники, и, соответственно безопасности полетов. В экстремальных условиях целесообразно стремиться к увеличению интенсивности эксплуатации, тем самым обеспечивается снижение продолжительности «глубоких» переходных циклов в охлаждении и приближение термического состояния ВС к оптимальным (желаемым) значениям его «эффективной температуры» (близкой к температуре полета - 20°С);
5) оптимальные значения характеристик интенсивности подогрева ВС в условиях поддержания ВС в диапазоне оптимальных значений «эффективной температуры» снижают время отрицательного термического воздействия на системы и оборудование ВС источников подогрева, что также способствует повышению безотказности авиационной техники.


