АВТОМАТИЧЕСКИЙ ЗАХОД НА ПОСАДКУ ПАЛУБНОГО САМОЛЕТА С ИСПОЛЬЗОВАНИЕМ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ
Содержание:
д. т. н., проф. В. В. Косьянчук, к. т. н. А. И. Наумов
(ВВИА им. Н.Е. Жуковского)
д. т. н., проф. Г. М. Синевич
(ОКБ им. Микояна)
Посадка на палубу авианесущего корабля (АК) является наиболее сложным и опасным этапом полета. По статистике ВМФ США более 50% авиационных происшествий происходит непосредственно при посадке.
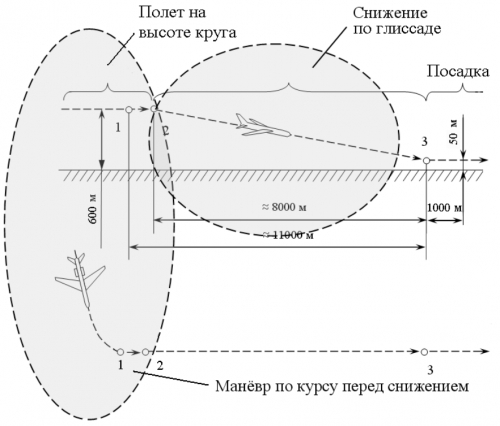
На рис. 1 показана траектория захода на посадку палубного самолета в вертикальной и горизонтальной плоскости.
Увеличить kosyanchuk12-2008-1.gif (68кб)
Рисунок 1. Траектория захода на посадку палубного самолета
Формирование этой траектории чаще всего осуществляется с использованием радиотехнической системы посадки, к аппаратурной и информационной надежности которой предъявляются высокие требования. Под информационным отказом будем понимать отказ (нарушение работоспособности) при отсутствии критических дефектов в корабельных и бортовых элементах системы [1]. В рассматриваемой задаче информационный отказ означает, что один из радиотехнических параметров, задающих траекторию движения самолета в процессе захода на посадку, формируется с повышенной погрешностью.
Параллельно с радиотехнической системой посадки на АК функционирует оптическая система посадки, которая дает возможность летчику визуально контролировать движение самолета по радиотехнической глиссаде, выявлять информационные отказы радиотехнической системы и выполнять заход на посадку в случае отказа радиотехнической системы. Достоинством оптической системы посадки является ее простота, а недостатки связаны с невозможностью реализации автоматического захода на посадку по данной системе, т.к. она предназначена для формирования качественной оценки местоположения ЛА относительно заданной линии глиссады.
Для повышения уровня безопасности полетов в случае отказов радиотехнической системы посадки в работе предлагается использовать системы технического зрения, широко внедряемые в настоящее время в бортовое оборудование ЛА [2, 3]. В данной статье будет рассмотрен алгоритм, позволяющий с использованием системы технического зрения и штатного закона управления самолета осуществить автоматический заход на посадку (без использования измерений радиотехнической системы посадки). Кроме того, выходная информация системы технического зрения может быть использована при проведении проверок и юстировок радиотехнической системы посадки.
Сформулируем суть предлагаемого подхода в концептуальном виде. На АК наносятся различимые маркерные точки, обладающие оптической контрастностью. На борту самолета устанавливается оптический датчик, обработка измерений которого позволяет определять относительные координаты точки установки датчика в корабельной системе координат, которые пересчитываются в угловое отклонение от заданной плоскости снижения (глиссады) εг опт и угловое отклонение от оси палубы εк опт, индекс «опт» здесь и далее имеет смысл «оптический».
Подавая сформированные сигналы εг опт и εк опт в закон управления вместо сигналов εг и εк, формируемых радиотехнической системой посадки, можно осуществлять автоматический заход на АК с использованием штатных законов управления, что особенно важно для современных ЛА, использующих сложные законы управления посадкой, вмешательство в которые недопустимо.
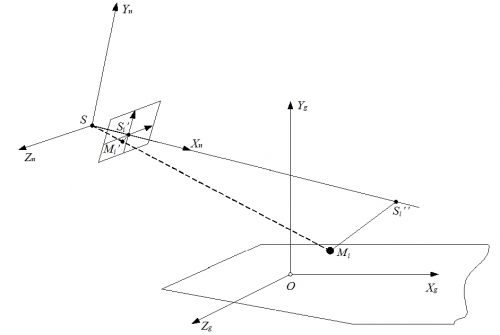
Предположим, что точка центра проектирования, реализуемого оптическим датчиком (телекамерой) на борту самолета, обозначена как S. Оптическая ось объектива камеры обозначена как SXи, в плоскости матричного фотоприемника расположены оси SYи и SZи, образующие в совокупности правую систему координат SXиYиZи (рис. 2). Эту систему координат будем называть лучевой системой координат оптического датчика.
Увеличить kosyanchuk12-2008-2.gif (7кб)
Рис. 2. «Земная» система координат АК и система координат датчика изображения
Помимо лучевой системы координат будем рассматривать также «земную» систему координат OXgYgZg, центр которой находится на подвижной посадочной платформе АК. Ось OXg для определенности будем ассоциировать с направлением продольной оси посадочной платформы, ось OYg - по нормали к платформе вверх, ось OZg дополняет систему координат до правой (рис. 2).
В соответствии с предположением о параметрах установки оптического датчика (телекамеры) на борту ЛА будем считать, что ось датчика отклонена от продольной строительной оси ЛА в плоскости симметрии фюзеляжа на фиксированный угол ε (положительное направление отсчета совпадает с положительным направлением для угла тангажа). Тогда матрица направляющих косинусов перехода от осей нормальной земной системы координат к осям лучевой системы координат может быть получена как последовательное произведение 4-х матриц элементарных поворотов:
- поворот на угол Δψ вокруг вертикальной оси; угол Δψ численно равен разности текущего угла рысканья и угла, составляемого осью OXg «земной» системы координат с направлением на истинный Север;
- поворот на угол тангажа ϑ вокруг поперечной оси;
- поворот на угол крена γ вокруг продольной оси;
- поворот на угол места ε вокруг поперечной оси.
Математически эта последовательность поворотов описывается следующим произведением матриц элементарных поворотов:
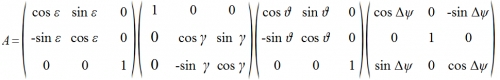
Увеличить kosyanchuk12-2008-3.gif (12кб)
что дает следующие выражения для элементов матрицы направляющих косинусов:

Увеличить kosyanchuk12-2008-4.gif (15кб)
Предположим, что нам известны координаты точки S=[x's y's z's]'T и нескольких маркерных точек Mi=[xi'm yi'm zi'm]'T в земной системе координат, i = 1,2,…; положение маркерных точек фиксировано в земной системе координат. Введем в рассмотрение вектора относительных дальностей точек Mi в проекциях на оси земной системы координат:
![]()
Увеличить kosyanchuk12-2008-5.gif (3кб)
В проекциях на оси лучевой системы координат SXиYиZи эти вектора будут иметь вид:
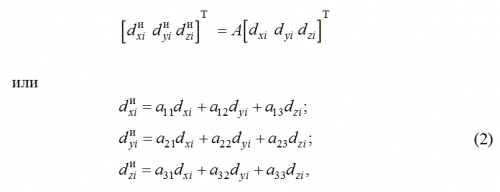
Увеличить kosyanchuk12-2008-6.gif (7кб)
где aij – элементы матрицы А.
Тогда, согласно геометрической схеме оптического измерения (рис. 2), можно записать следующие уравнения для координат проекции точки Мi на экранную плоскость матрицы [yэi zэi]'T (т.е. для точки Si' в системе координат SXиYиZи) [2]:
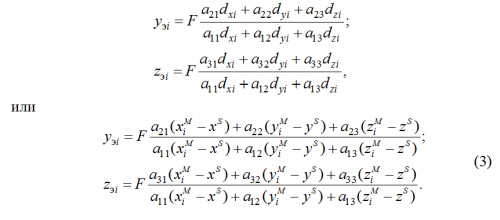
Увеличить kosyanchuk12-2008-7.gif (13кб)
Измерение координат центров изображений маркированных точек выполняется с некоторыми ошибками: yэi~ = yэi + δyi, zэi~ = zэi + δzi. Подставив данные измерения в уравнения (3), получаем систему нелинейных алгебраических уравнений относительно неизвестных координат точки S и углов пространственной ориентации ЛА:
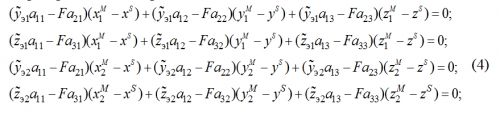
Увеличить kosyanchuk12-2008-8.gif (13кб)
. . .
Минимальное число маркерных точек, для которого удовлетворяются необходимые условия разрешимости системы уравнений, – 3. При этом имеется 6 нелинейных уравнений относительно 6 неизвестных, для решения которых может быть применен метод Ньютона [3]. В результате будут получены координаты искомой точки S=[x's y's z's]'T, а также углов Δψ, ϑ, γ.
Используя координаты точки S, можно определить эквивалентные угловые отклонения самолета εг опт, εк опт от заданной линии глиссады:
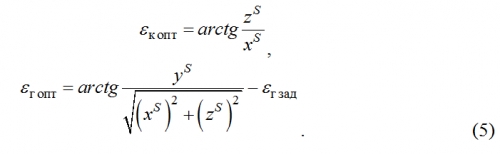
Увеличить kosyanchuk12-2008-9.gif (4кб)
Проверка работоспособности предлагаемого подхода осуществлялась численным моделированием и проводилась в два этапа.
На первом этапе исследовались особенности предлагаемого алгоритма вычисления εг опт, εк опт для различных начальных условий и шумов оптических измерений. На втором этапе проводилось моделирование автоматического захода на посадку на АК с использованием штатных законов управления палубного самолета.
Для исследований первого этапа в качестве исходных данных использовались 3 маркерные точки с координатами: (-100, 0, 20); (-100, 0, -20); (0, 50, 0). Будем считать, что истинные значения координат точки S равны (-4000, 200, 15), пространственное положение самолета характеризуется углами Δψ = 0,05 рад, ϑ = 0,05 рад, γ = 0.
Для решения системы нелинейных уравнений (4) использовалась функция fsolve языка МatLab.
Было рассмотрено 3 характерных случая.
В первом случае в качестве начального приближения итерационного решения выбирались точки с нулевыми значениями координат и углов пространственной ориентации, что соответствует случаю полной априорной неопределенности при получении решения. Численное решение получено за 52 итерации, погрешность решения (абсолютная ошибка –|x вычисл - x истин|) не превысила величины 10'-11 ст.
Во втором случае в качестве начальной точки использовались измененные на 10% значения точных координат местоположения и углового положения самолета x's, y's, z's, Δψ, ϑ, γ, что соответствует случаю частичной априорной неопределенности. Численное решение получено за 9 итераций, погрешность решения осталась на уровне 10'-11 ст.(абсолютная ошибка).
В третьем случае были сохранены условия задания начальной точки во втором случае, но добавлено систематическое смещение по всем координатам x's на 1%, характеризующее ошибку датчиков. В результате численное решение было получено за 9 итераций, но абсолютная погрешность численного решения по координатам составила 0,1908 м, 1,9722 м, 0,2083 м, что является приемлемым результатом для истинных координат -4000 м, 200 м, 15 м и не превосходит 1%-ю относительную ошибку. Увеличение систематического смещения по всем координатам x's до 5% приводит к ошибкам 0,9034 м, 9,4796 м, 0,9862 м, что не превосходит 5%-й относительной ошибки.
Вычислительные затраты на решение системы уравнений (4) во многом определяются удалением исходной точки (3 линейных координаты и 3 угла) итерационного поиска от точки решения. В рассматриваемой задаче информационного обеспечения посадки сокращение вычислительных затрат может быть обеспечено с привлечением дополнительной информации о местонахождении и угловой ориентации ЛА. При этом следует рассматривать 2 случая:
- на борту ЛА имеется система счисления пути и датчики пространственной ориентации, характеризующиеся своими ошибками измерения; в этом случае в качестве исходной точки итерационного поиска следует брать показания бортовых систем, а полученное решение использовать в бортовом алгоритме комплексной обработки пилотажно-навигационной информации;
- на борту ЛА не имеется бортовых измерителей, в этом случае в качестве исходной точки итерационного поиска следует брать решение, полученное на предыдущем цикле функционирования алгоритма обработки измерений оптического датчика.
Отметим, что 2-й случай (как более общий), позволяет добиться сокращения вычислительных затрат в 7 - 9 раз по сравнению со случаем, когда исходная точка задавалась в начале земной системы координат без привлечения дополнительной информации.
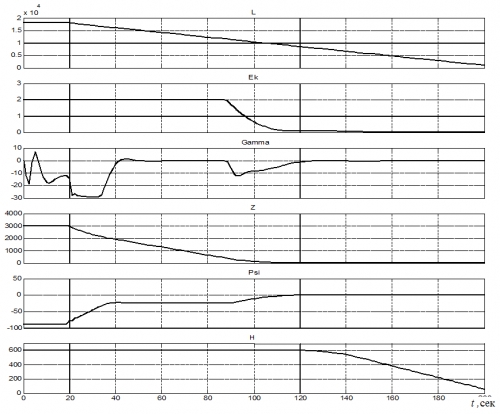
Моделирование автоматического захода на посадку осуществлялось с использованием полной нелинейной модели гипотетического палубного самолета. Результаты моделирования представлены на рис. 3. Из рис. 3 видно, что летательный аппарат заходит на АК с курсом – 90° на дальности 18000 м. На дальности приблизительно 11000 м начинается обработка измерений оптического датчика, в результате которой формируются угловые отклонения εг опт, εк опт. Эти параметры подаются в закон управления, графики для бокового отклонения Z и текущей высоты H характеризуют движение самолета со штатными законами автоматического управления и «оптическим» информационным обеспечением. Процесс автоматического захода на посадку заканчивается при дальности до корабля L=1000 м, высоте H=50 м. В условиях отсутствия внешних возмущений боковое отклонение составило Z=0 м, углы и угловые отклонения Δψ=0, γ=0, εг опт=0, εк опт=0.
Увеличить kosyanchuk12-2008-10.gif (14кб)
Рис. 3 Результаты моделирования
Таким образом, результаты моделирования показывают, что предлагаемый подход позволяет осуществлять автоматический заход на посадку с использованием оптического датчика и штатной системы управления палубного самолета.
Работа выполнена при поддержке гранта РФФИ № 06-08-01497-а.
1. Дмитриев С. П., Колесов Н. В., Осипов А. В. Информационная надежность, контроль и диагностика навигационных систем. СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 2004.
2. Fitzgerald, Daniel L. and Mejias, Luis O. and Eng, Pillar C. and Liu, Xi and Walker, Rodney A. Towards Flight Trials for an Autonomous UAV mergency Landing using Machine Vision. In Proceedings Australasian Conference on Robotics and Automation, Brisbane. 2007.
3. Белоглазов И. Н., Казарин С. Н. Автоматическое стереоскопическое распознавание наблюдаемых сцен. // Изв. РАН. Теория и системы управления. 1999, № 6.
4. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. М.: Наука, 1986 г.