АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЦЕЛЕВОЙ ФУНКЦИИ МЕТОДОМ ГРУППОВОГО УЧЕТА АРГУМЕНТОВ
В статье рассматривается один из методов моделирования, основанный на принципе самоорганизации априорной информации, построении конкурирующих моделей и выборе из них рационального варианта при решении оптимизационных задач.
Аналитическое представление целевой функции методом группового учета аргументов
Индуктивный метод моделирования, основанный на принципе самоорганизации, исходит из минимального объема требуемой для моделирования априорной информации. Высокая точность аппроксимирующих функций достигается при помощи перебора большого числа вариантов моделей по выбранным внешним критериям.
Критерий называется внешним, если его определение основано на новой информации «свежих» точек, неиспользованных при синтезе модели. Согласно теореме Геделя из математической логики о необходимости внешнего заполнения, только внешние критерии позволяют выбрать единственную (для каждого критерия) модель оптимальной сложности. Любой внутренний критерий сравнения моделей приводит к ложному правилу: чем сложнее модель, тем она точнее.
Принцип самоорганизации состоит в том, что при постепенном усложнении моделей внешние критерии проходят через свой минимум, который и соответствует оптимальной структуре модели.
В самом общем виде алгоритм индуктивного метода самоорганизации моделей можно представить состоящими из генератора моделей, на выходе в определенном порядке повышения сложности получаются варианты (претенденты) моделей, и селектирующего устройства, выбирающего по заданному критерию рациональную модель.
Наиболее известным и широко применяемым является многорядный алгоритм селекции, который называется методом группового учета аргументов (МГУА). Его можно применять, когда таблица данных содержит всего (10...20) точек, для поиска модели с числом коэффициентов, во много раз превышающих число исходных данных.
В зависимости от свойств объекта выбирается тот или иной вид аппроксимирующей модели. Вид аппроксимирующей модели носит название опорной функции. В качестве опорных функций применяются формулы Байеса, гармоническая, логарифмическая или степенная функции. Наибольшее распространение получили последние из них, причем в МГУА используются в основном полиномиальные модели, например, шестичленного вида:
![]()
Увеличить ruhlinskiy10-2008-01.gif (3кб)
На основании вида опорной функции в первом ряду селекции образуются все возможные пары аргументов и для каждой из них находится частная модель вида:
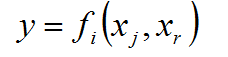
(2)
для любой возможной парной дизъюнкции аргументов.
После генерации частных моделей для всех возможных парных дизъюнкций аргументов на первом ряду селекции производится их сортировка (отбор) по выбранному внешнему критерию регулярности. Под регулярностью модели понимается степень ее применения для описания объекта при произвольных сочетаниях аргументов из заданного неравенством
![]()
n-мерного пространства.
В качестве критерия регулярности, по которому оценивается степень компетентности полинома – претендента, может быть рекомендована:
- относительная среднеквадратическая ошибка:
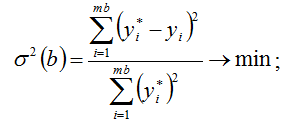
- коэффициент корреляции:
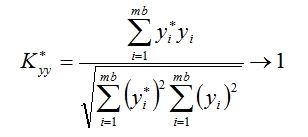
- индекс корреляции:
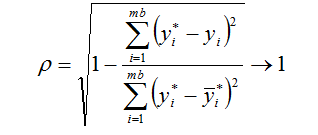
- критерии несмешанности:
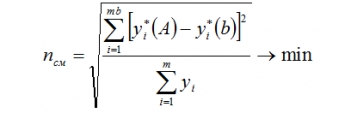
Увеличить ruhlinskiy10-2008-07.gif (3кб)
где
![]()
полученные по модели и действительные значения (сходной величины в i -точке;
![]()
- математическое ожидание выходной величины полинома.
Для получения коэффициентов частных полиномов и их последующей сортировки по внешним критериям исходная таблица данных, полученная с помощью ТПЭ и реального или математического эксперимента, разделена на две части:
- обучающую (В), по которой производится вычисление коэффициентов;
- проверочную (А) или экзаменационную, по которой производится сортировка (отбор) полиномов-претендентов (расчет внешних критериев).
Рекомендуемое соотношение для разделения опытных данных может быть следующее:
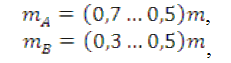
где m - общее число точек исходной информации.
Наиболее простая процедура разделения исходной информации на обучающую и проверочную состоит в следующем:
1) исходную таблицу делят на две части. В первую заносят все данные с нечетными номерами опытов, во вторую – с четными номерами;
2) вычисляют дисперсию той и другой части по формуле:
![]()
Увеличить ruhlinskiy10-2008-11.gif (5кб)
3) часть данных с большим значением дисперсии назначается обучающей, а вторая – проверочной.
Кроме оценки претендентов по значениям перечисленных критериев, рекомендуется учитывать сходимость процесса итерационного уточнения при решении системы линейных уравнений для вычисления коэффициентов полиномов опорных функций.
Критерием сходимости решения является степень обусловленности матрицы. Если процесс решения расходящейся, матрица считается плохо обусловленной, и такой претендент при сортировке отсеивается.
При проведении отбора претендентов на каждом ряду селекции рекомендуется учитывать следующие два положения:
1) предпочтительное число претендентов, признанных лучшими при отборе и прошедших на следующий ряд селекции, должно быть постоянным и равным числу входных переменных (аргументов) первого ряда:
![]()
Увеличить ruhlinskiy10-2008-12.gif (2кб)
где
S - номер ряда селекции;
F - число лучших по критерию селекции полиномов;
2) при отборе на каждом ряду селекции необходимо осуществлять протекцию всех входных переменных.
Применяя методику исследования аппроксимирующих зависимостей с помощью метода группового учета аргументов по статистическому материалу, полученному в результате машинного эксперимента для каждой совокупности варьируемых параметров из матрицы планирования (табл. 1), определены аналитические выражения для целевой функции, представляющие собой систему уравнений частных описаний шестичленных полиномов второй степени.
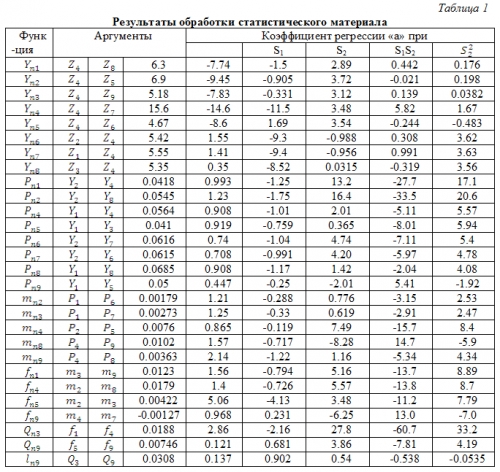
Увеличить ruhlinskiy10-2008-13.gif (42кб)
Следует отметить, что в соответствии с МГУА статистический материал (≈60 опытов) делится на три части: общую – с 1-го по 20-ый опыт, проверочную – с 21-го по 40-ой опыт и экзаменационную – с 41-го до 60-ый опыт.
Первая группа опытов использовалась для получения коэффициентов полиномов частных описаний на каждом пороге отбора, вторая – для селекции претендентов описании при отборе по внешним критериям, а третье – для проверки прогнозирующих свойств (регулярности) полученной аналитической зависимости.
На основании проведенного ранее параметрического и регрессионного анализа с использованием гистограмм влияния и диаграмм рассеивания варьируемых параметров для функций ограничения выбраны в качестве аргументов полиномов доминирующие факторы. В результате для x1,x4,x5,x6 – описания целевой функции были выбраны девять аргументов: неуправляемых x2,x6,x7; управляемых x10,x11,x12,x14,x15,x16.
![]()
Увеличить ruhlinskiy10-2008-14.gif (4кб)
где
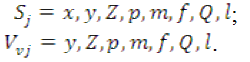
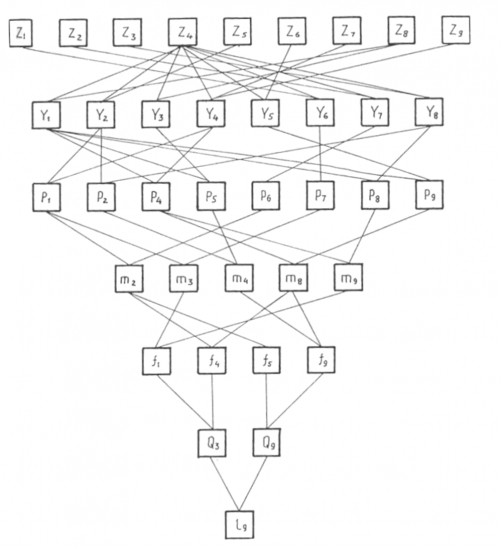
Увеличить ruhlinskiy10-2008-16.gif (182кб)
Рис. 1. Граф целевой функции
Значения коэффициента разложения частных полиномов для целевой функции приведены в табл. 2.

Увеличить ruhlinskiy10-2008-17.gif (20кб)
Если осуществить последовательную подстановку всех частных полиномов с исключением промежуточных переменных
![]()
, то может быть получен полный полином 64 степени от 9 аргументов, который содержит 168 членов. Однако в численных расчетах целесообразно использовать несвернутую систему уравнений частных описаний с последовательным вычислением их с помощью компактной вычислительной процедуры, состоящей из вложенных друг в друга циклов. В этом случае вычисление целевой функции осуществляется на ЭВМ за 0,2 с при малой (порядка 10 Кбайт) потребности памяти машины.
Полученное аналитическое выражение целевой функции, несмотря на чрезвычайно малое количество исходной информации (всего лишь 60 опытов), обладает высокими аппроксимирующими и прогнозирующими свойствами. Индекс корреляции и среднеквадратичное отклонение, вычисленные по всем опытам (для аппроксимации) и по половине опытов (для регулярности), достигают высокого уровня
![]()
(рис. 2).
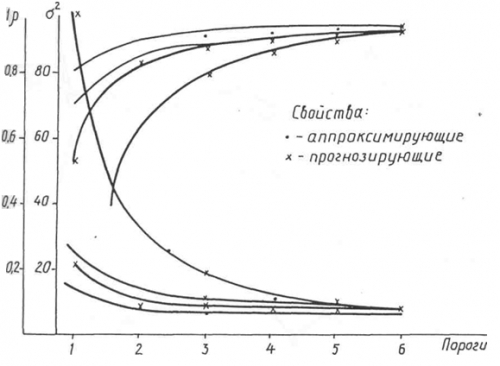
Увеличить ruhlinskiy10-2008-20.gif (50кб)
Рис. 2. Индекс корреляции и среднеквадратичное отклонение
Сравнение фактического и расчетного значений целевой функции (по полиному) приведено на рис. 3, где показано хорошее совпадение как для обучающих опытов, по которым проведены расчеты коэффициентов частным полиномов, так и для проверочных, по которым определялись критерии отбора, а также и для экзаменационной группы опытов, которая не принимала участия в формировании функции.
а) Проверочные опыты

Увеличить ruhlinskiy10-2008-21.gif (17кб)
б) Обучающие опыты

Увеличить ruhlinskiy10-2008-22.gif (24кб)
в) Экзаменационные опыты
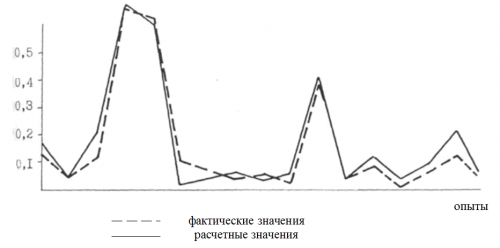
Увеличить ruhlinskiy10-2008-23.gif (23кб)
Рис. 3. Сравнение фактического и расчетного значений целевой функции



